12. 레드블랙트리
– 레드-블랙 트리
- 이진탐색트리의 일종
- 균형잡힌 트리 : 높이가 O(logn)
- SEARCH, INSERT, DELETE 연산을 최악의 경우에도 O(logn) 시간
- 각 노드의 하나의 키(key), 왼쪽자식(left), 오른쪽 자식(right) 그리고 부모노드(p)의 주소를 저장
- 자식노드가 존재하지 않을 경우 NIL 노드라고 부르는 특수한 노드가 있다고 가정
- 따라서 모든 리프노드는 NIL노드라고 가정
- 노드들은 내부노드와 NIL 노드로 분류
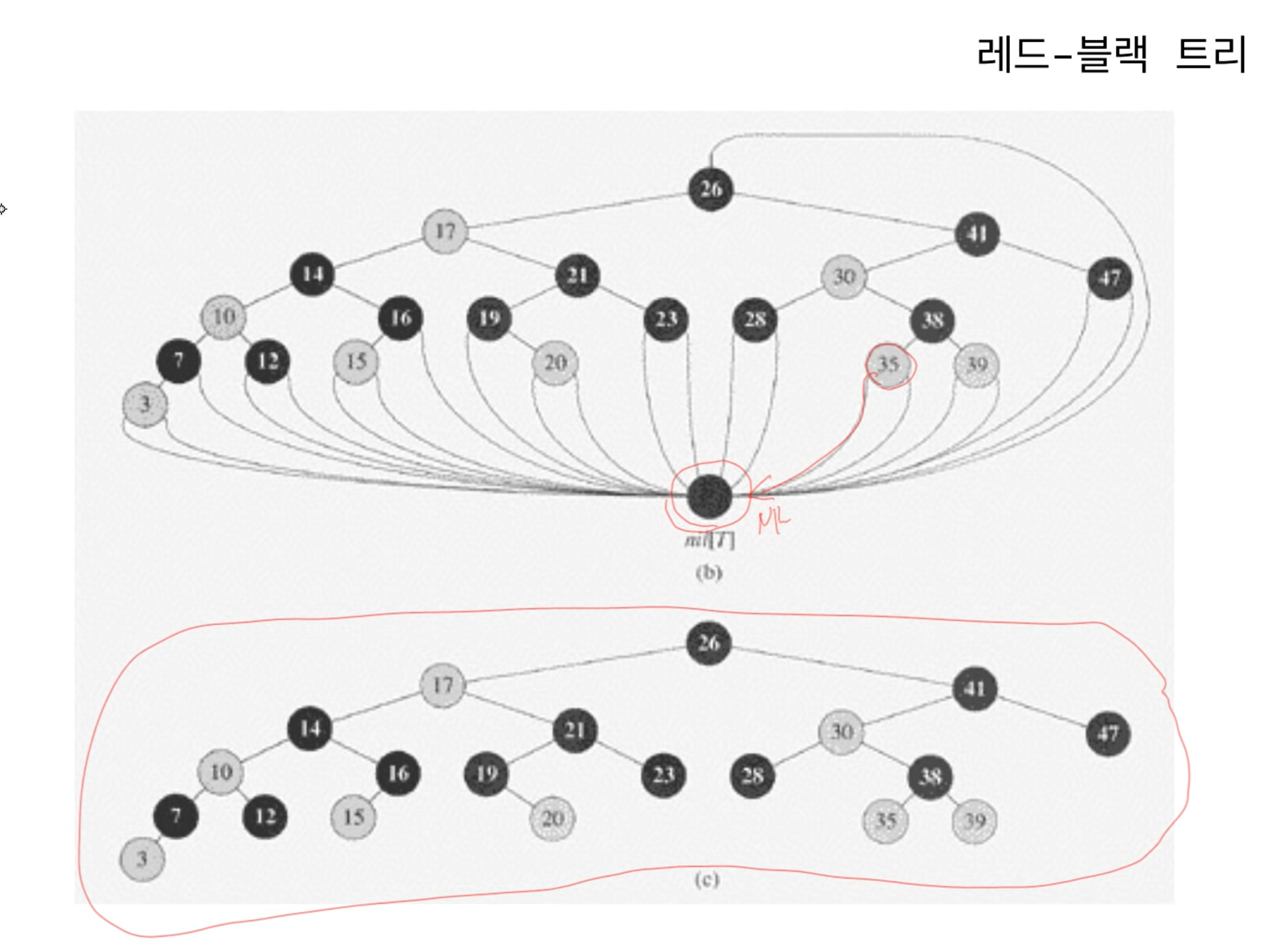
레드-블랙 트리 : 정의
- 다음의 조건을 만족하는 이진탐색트리 :
1. 각 노드는 red 혹은 black이고,
2. 루트노드는 black이고,
3. 모든 리프노드(즉, NIL노드)는 black이고,
4. red노드의 자식노드들은 전부 black이고(즉, red노드는 연속되어 등장하지 않고)
5. 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
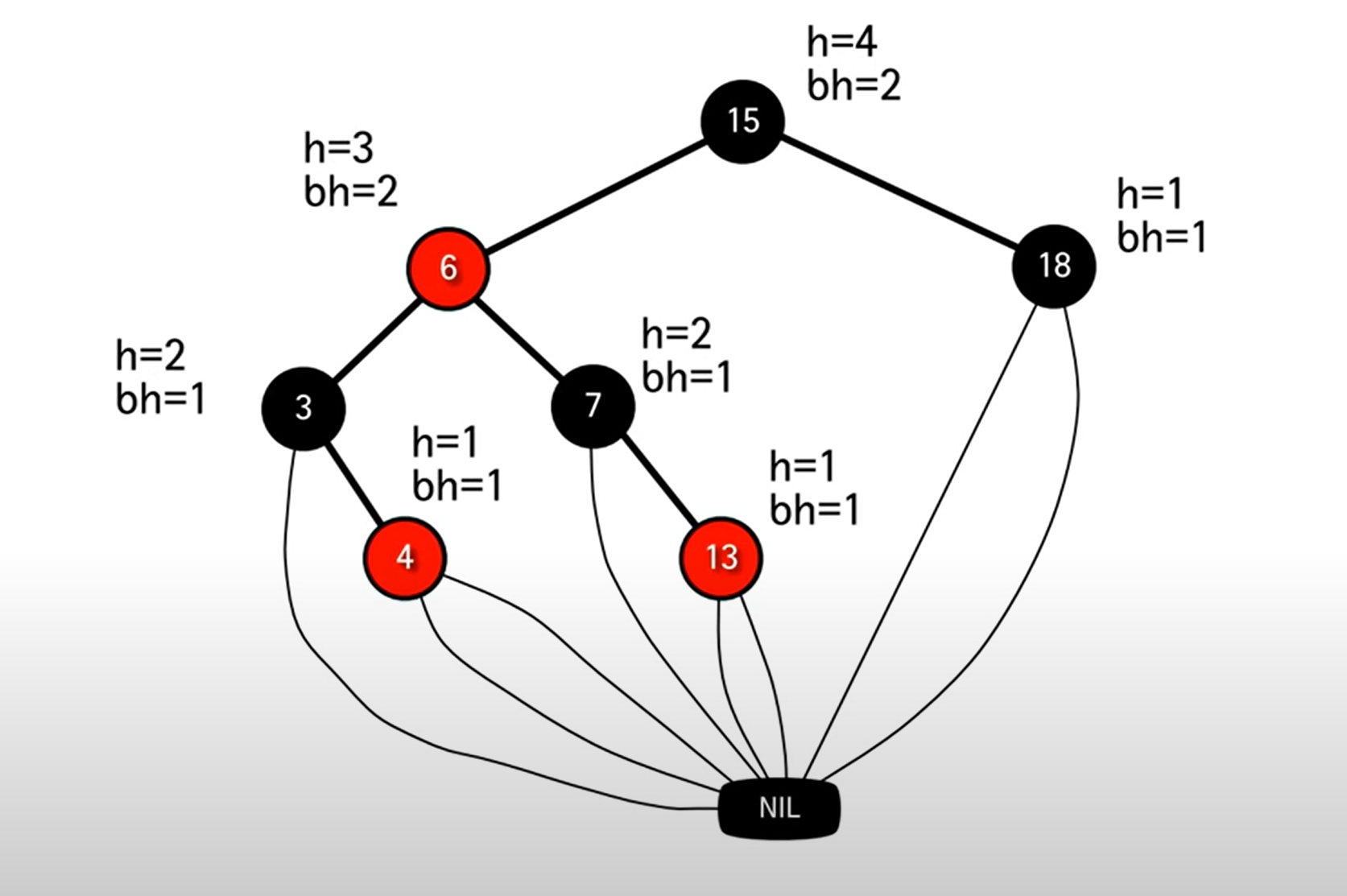
레드-블랙 트리의 높이
노드 x의 높이 h(x)는 자신으로부터 리프노드까지의 가장 긴 경로에 포함된 에지의 개수이다.
노드 x의 블랙-높이 bh(x)는 x로부터 리프노드까지의 경로상의 블랙노드의 개수이다(노드 x 자신은 불포함)
높이가 h인 노드의 블랙-높이는 bh>=h/2이다 (조건 4에 의해 리드노드는 연속될 수 없으므로 당연)
노드 x를 루트로하는 임의의 부트리는 적어도 2^(bh(x))-1개의 내부노드를 포함한다(수학적귀납법)
n개의 내부노드를 가지는 레드블랙트리의 높이는 2log(n+1)이하이다(n>=2^(bh)-1>=2^(h/2)-1이므로, 여기서 bh와 h는 각각 루트 노드의 블랙-높이와 높이)
Left and Right Rotation
시간복잡도 O(1)
이진탐색트리의 특성을 유지

– Left Rotation
y = right[x] ≠ NIL 이라고 가정
루트노드의 부모도 NIL이라고 가정
LEFT-RATATE(T,x)
y <- right[x] //set y
right[x] <- left[y] // Turn y's left subtree into x's right subtree
p[left[y]] <- x
p[y] <- p[x] // Link x's parent to y
if p[x] = nil[T]
then root[T] <- y
else if x = left[p[x]]
then left[p[x]] <- y
else right[p[x]] <- y
left[y] <- x // Put x on y's left
p[x] <- y
– INSERT
보통의 BST에서처럼 노드를 INSERT한다
새로운 노드 z를 red노드로 한다
RB-INSERT-FIXUP을 호출한다
RB-INSERT(T,z)
y <- nil[T]
x <- root[T]
while x ≠ nil[T]
do y <- x
if key[z] < key[x]
then x <- left[x]
else x <- righ[x]
p[z] <- y
if y == nil[T]
then root[T] <- z
else if key[z] < key[y]
then left[y] <- z
else right[y] <- z
left[z] <- nil[T]
right[z] <- nil[T]
color[z] <- RED
RB-INSERT-FIXUP(T,z)RB-INSERT-FIXUP
위반될 가능성이 있는 조건들
1. ok
2. 만약 z가 루트노드라면 위반, 아니라면 ok
3. ok
4. z의 부모 p[z]가 red 이면 위반
5. ok
경우1 : z의 삼촌이 red
조건 2와 4 이외의 조건들은 여전히 ok이면서 z가 두칸 위로 올라감
경우2 : z가 오른쪽 자식인 경우(z의 삼촌이 black)
p[z]에 대해서 left-rotation한 후 원재 p[z]를 z로
경우 3으로
경우3 : z가 왼쪽 자식인 경우(z의 삼촌이 black)
p[z]를 black, b[p[z]]를 red로 바꿈
p[p[z]]에 대해서 right-rotation
경우 4,5,6
경우 1,2,3은 p[z]가 p[p[z]]의 왼쪽 자식인 경우들
경우 4,5,6은 p[z]가 p[p[z]]의 오른쪽 자식인 경우
경우 1,2,3과 대칭적이므로 생략
RB-INSERT-FIXUP
RB-INSERT-FIXUP(T,z)
while color[p[z]] == RED
do if p[z] = left[p[p[z]]]
then y <- right[p[p[z]]]
if color[y] = RED
then color[p[z]] <- BLACK // Case 1
color[y] <- BLACK // Case 1
color[p[p[z]]] <- RED // Case 1
z <- p[p[z]]
else if z = right[p[z]]
then z <- p[z] // Case 2
LEFT-ROTATE(T,z) // Case 2
color[p[z]] <- BLACK // Case 3
color[p[p[z]]] <- RED // Case 3
RIGHT-ROTATE(T,p[p[z]]) // Case 3
else (same as then clause with "right" and "left" exchanged)
color[root[T]]<-BLACK
INSERT의 시간복잡도
- BST에서의 INSERT : O(logn)
- RB-INSERT-FIXUP
경우1,(4)에 해당할 경우 z가 2레벨 상승
경우 2,3,(5,6)에 해당할 경우 O(1)
따라서 트리의 높이에 비례하는 시간
- 즉, INSERT의 시간복잡도는 O(logn)
– DELETE
보통의 BST에서처럼 DELETE한다
실제로 삭제된 노드 y가 red였으면 종료
y가 black이었을 경우 RB-DELETE-FIXUP을 호출한다.
RB-DELETE(T,z)
if left[z] == nil[T] or right[z] == nil[T]
then y <- z
else y <- TREE-SUCCESSOR(z)
if left[y] ≠ nil[T]
then x <- left[y]
else x <- right[y]
p[x] <- p[y]
if p[y] = nil[T]
then root[T] <- x
else if y == left[p[y]]
then left[p[y]] <- x
else right[p[y]] <- x
if y ≠ z
then key[z] <- key[y]
copy y's satellite data into z
if color[t] = BLACK
then RB-DELETE-FIXUP(T,x)
return y
RB-DELETE-FIXUP
위반될 가능성이 있는 조건들
1. ok
2. y가 루트였고 x가 red인 경우 위반
3. ok
4. p[y]와 x가 모두 red일 경우 위반
5. 원래 y를 포함했던 모든 경로는 이제 black노드가 하나 부족
1) 노드 x에 "extra black"을 부여해서 일단 조건 5를 만족
2) 노드 x는 "double black" 혹은 "red&black"
아이디어
extra black을 트리의 위쪽으로 올려보냄
x가 red&black상태가 되면 그냥 black노드로 만들고 끝냄
x가 루트가 되면 그냥 extra black을 제거
Loop Invariant
x는 루트가 아닌 double-black노드
w는 x의 형제노드
w는 NIL 노드가 될 수 없음(아니면 x의 부모에 대해 조건 5가 위반)
경우1 : w가 red인 경우
w의 자식들은 black
w를 black으로, p[x]를 red로
p[x]에 대해서 left-rotation적용
x의 새로운 형제노드는 원래 w의 자식노드, 따라서 black노드
경우 2,3, 혹은 4에 해
경우2 : w는 black, w의 자식들도 black
x의 extra-black을 뺏고, w를 red로 바꿈
p[x]에게 뺏은 extra-black을 준다
p[x]를 새로운 x로 해서 계속
만약 경우1에서 이 경우에 도달했다면 p[x]는 red였고, 따라서 새로운 x는 red&black이 되어서 종료
경우3. w는 black, w의 왼쪽자식이 red
w를 red로, w의 왼자식을 black으로
w에 대해서 right-rotation적용
x의 새로운 형제 w는 오른자식이 red: 경우 4에 해당
경우4. w는 black, w의 오른쪽자식이 red
w의 색을 현재 p[x]의 색으로(unknown color)
p[x]를 black으로, w의 오른자식을 black으로
p[x]에 대해서 left-rotation적용
x의 extra-black을 제거하고 종료
경우 5,6,7,8
경우 1,2,3,4는 x가 왼쪽 자식인 경우
경우 5,6,7,8은 x가 p[x]의 오른쪽 자식인 경우
경우 1,2,3,4와 각각 대칭적임
RB-DELETE-FIXUP
RB-DELETE-FIXUP(T,x)
while x ≠ root[T] and color[x] = BLACK
do if x = left[p[x]]
then w <- right[p[x]]
if color[w] = RED
then color[w] <- BLACK // Case 1
color[p[x]] <- RED // Case 1
LEFT-ROTATE(T,p[x]) // Case 1
w <- right[p[x]] // Case 1
if color[left[w]] = BLACK and color[right[w]]=BLACK
then color[w] <- RED // Case 2
x <- p[x] // Case 2
else if color[right[w]] = BLACK
then color[left[w]] <- BLACK // Case 3
color[w] <- RED // Case 3
RIGHT-ROTATE(T,w) // Case 3
w <- right[p[x]] // Case 3
color[w] <- color[p[x]] // Case 4
color[p[x]] <- BLACK // Case 4
color[right[w]] <- BLACK // Case 4
LEFT-ROTATE(T,p[x]) // Case 4
x <- root[T] // Case 4
else (same as then clause with "right" and "left" exchanged)
color[x] <- BLACK
DELETE의 시간복잡도
- BST에서의 DELETE : O(logn)
- RB-DELETE-FIXUP : O(logn)
'공부기록 > 알고리즘' 카테고리의 다른 글
| [알고리즘]P1713. 후보 추천하기 (0) | 2024.02.14 |
|---|---|
| [알고리즘] P2143. 두 배열의 합 (0) | 2024.02.14 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch2.이진검색트리 (0) | 2023.08.05 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch1.정렬 #8~11 (0) | 2023.08.05 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch1.정렬 #1~7 (0) | 2023.07.29 |

