섹션 1. 정렬
7. 정렬의 lower bound
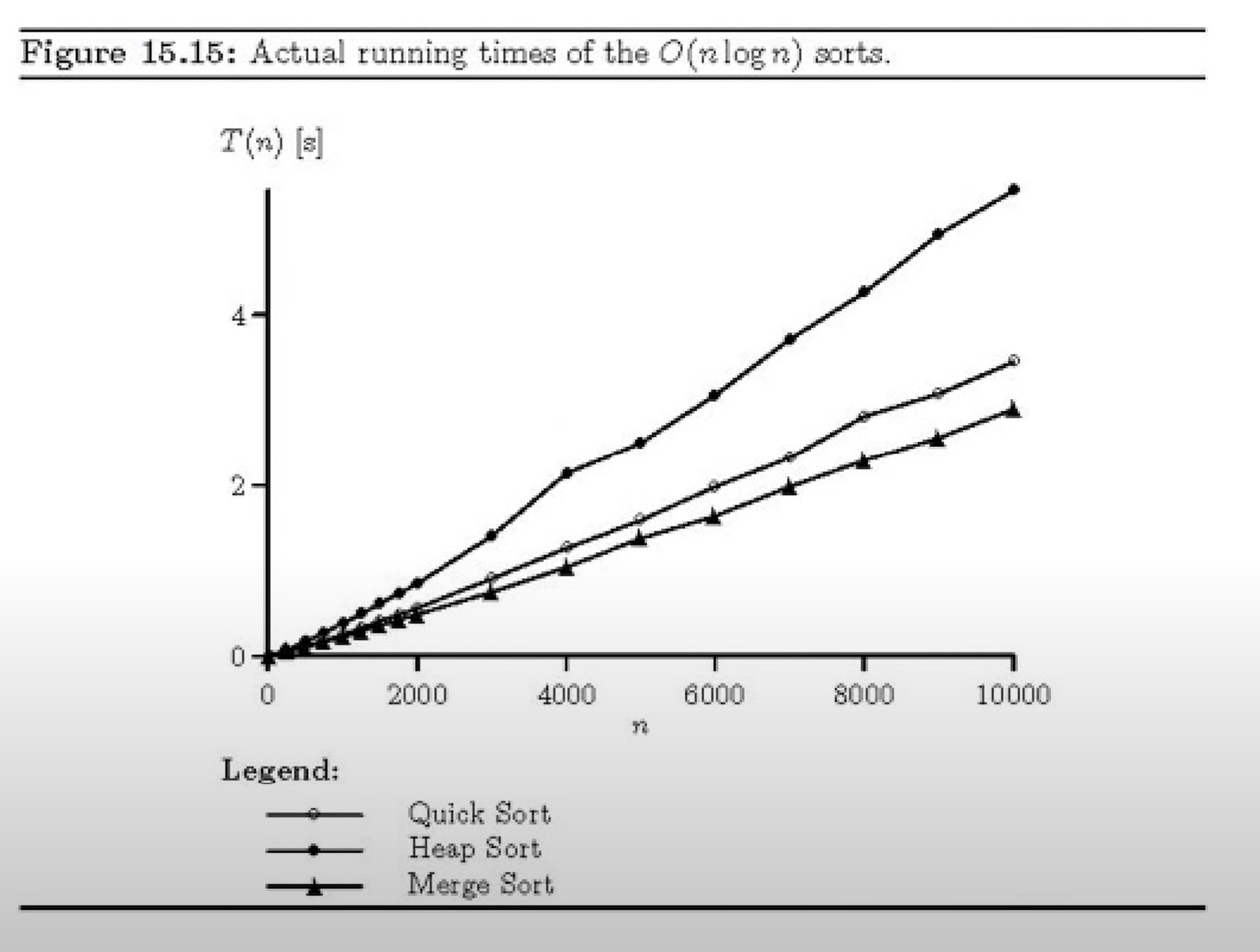
저번에 배웠던 정렬 알고리즘!
nlogn 이 최선일까?
결론 : O(nlogn) 보다 더 작아질 수는 없다(comparison sort 인 경우에는!)
| 정렬 알고리즘 | |
| - Bubble sort - Insertion sort - Selection sort |
simple, slow |
| - Quicksort - Merge sort - Heap sort |
fast |
| - Radix sort | O(N) |
– Comparision sort
- 데이터들간의 상대적 크기관계만을 이용해서 정렬하는 알고리즘
- 따라서 데이터들간의 크기 관계가 정의되어 있으면 어떤 데이터에든 적용가능(문자열, 알파벳, 사용자 정의 객체 등)
- 버블 소트, 삽입 정렬, 합병 정렬, 퀵소트, 힙정렬 등
- Non-comparison sort
정렬할 데이터에 대한 사전지식을 이용 - 적용에 제한 (ex)Bucket sort, Radix sort)
- 하한(Lower bound)
입력된 데이터를 한번씩 다 보기위해서 최소 O(n)의 시간복잡도 필요
합병정렬과 힙정렬 알고리즘들의 시간복잡도는 O(nlogn)
어떤 comparision sort 알고리즘도 O(nlogn)보다 나을 수 없다
DECISION Tree(Abstraction of any comparision sort)
자식이 없는 노드(leaf node) 의 갯수는? n!개 (leaf 노드들은 다 서로다른 결과이니까)

- Leaf 노드의 개수는 n!개. 왜냐하면 모든 순열(permutation)에 해당하므로
- 최악의 경우 시간복잡도는 트리의 높이에 비
- 트리의 높이는 height >= logn! = O(nlogn)
8. 선형시간 정렬 알고리즘
-Counting sort
n개의 정수를 정렬하라. 단 모든 정수는 0에서 k사이의 정수이다(사전지식) ex: k : 비교적 작을 때
예 : n명의 학생들의 시험점수를 정렬하라. 단 모든 점수는 100이하의 양의 정수이다.
길이 k인 배열에 각 정수의 개수를 count 한다.
int A[n]; // 정렬할 데이터 (0에서 k사이의 정수니까)
int C[k] = {0,};
for (int i = 1; i<=n; i++)
C[A[i]]++;
for (int s=1, i=0; i<=k; i++){
for(int j=0; j<C[i];j++){
A[s++]=i;
}
}Is it okay? -> no. 대부분의 경우 정렬할 key값들은 레코드의 일부분이기 때문
숫자들은 정렬이 되겠지만, 큰 데이터의 일부분이기 때문에 안될거야
- 최종 코드
COUNTING-SORT(A,B,k)
for i <-0 to k
do C[i] <- 0
for j <- 1 to length[A]
do C[A[j]] <- C[A[j]] + 1
> C[i] now contains the number of elements equal to i
for i <- 1 to k
do C[i] <- C[i] + C[i-1]
> C[i] now contains the number of elements less than or equal to i
for j <- length[A] downto 1
do B[C[A[j]]] <- A[j]
C[A[j]] <- C[A[j]] - 1O(n+k) (n>k) , 또는 O(n) if k = O(n)
k가 클 경우 비실용적
stable 정렬 알고리즘
> "입력에 동일한 값이 있을 때 입력에 먼저 나오는 값이 출력에서도 먼저 나온다"
> Counting 정렬은 stable하다
- Radix sort
n개의 d자리 정수들
가장 낮은 자리수부터 정렬
RADIX-SORT(A,d) // n개 배열, dwkfl 함수
for i <- 1 to d
do use a stable sort to sort array A on digit i시간복잡도 O(d(n+k))
| 정렬 알고리즘 | |
| Bubble sort Insertion sort Selection sort |
O(n^2) O(n^2) O(n^2) |
| Quicksort |
worst O(n^2) and average O(nlogn) |
| Merge sort | O(nlogn) |
| Heap sort | O(nlogn) |
| Counting sort Radix sort |
O(n+k) O(d(n+k)) |


9. sorting in java
- 기본 타입 데이터의 정렬
Arrays 클래스가 primitive 타입 데이터를 위한 정렬 메서드를 제공
int [] data = new int [capacity];
//data[0]에서 data[capacity-1]까지 데이터가 꽉 차있는 경우에는 다음과 같이 정렬한다.
Arrays.sort(data);
//배열이 꽉차있지 않고 data[0]에서 data[size-1]까지 size개의 데이터만 있다면 다음과 같이 한다.
Arrays.sort(data,0,size);-int 이외의 다른 primitive 타입 데이터(double, char 등)에 대해서도 제공
- 객체의 정렬 : 문자열
primitive 타입 데이터와 마찬가지로 Arrays.sort 메서드로 정렬된다.
-ArrayList 정렬 : 문자열
collections.sort 메서드로 정렬된다
- 객체의 정렬 : 사용자 정의 객체
어떤 걸 기준으로 정렬할지를 규칙을 정의해줘야한다.
// 이름을 기준으로 정렬
public int compareTo(Fruit other){
return name.compareTo(other.name);
}
// 재고수량으로 정렬
public int compareTo(Fruit other){
return quantity - other.quantity;
}
//두 가지 기준을 동시에 지원하려면 Comparator 사용
//comparator 클래스를 extends하며 compare 메서드를 overriding 하는 새로운 이름 없는 클래스를 정의한 후
//그 클래스의 객체를 하나 생성한다
Comparator<Fruit> nameComparator = new Comparator<Fruit>(){
public int compare(Fruit fruit1, Fruit fruit2) {
return fruit1.name.compareTo(fruit2.name);
}
};데이터 객체의 static member로 둔다. 정렬할 때는
Arrays.sort(fruits, Fruit.nameComparator);
'공부기록 > 알고리즘' 카테고리의 다른 글
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch3.레드블랙트리 (0) | 2023.08.12 |
|---|---|
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch2.이진검색트리 (0) | 2023.08.05 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch1.정렬 #1~7 (0) | 2023.07.29 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch0.순환 #4~7 (0) | 2023.07.22 |
| 영리한 프로그래밍을 위한 알고리즘 강좌 - Ch0.순환 #1~3 (0) | 2023.07.22 |


